2025-09-17 20:58
Tags: 경제학
전망이론
-
인간은 동일한 크기의 이익에서 얻는 기쁨보다 손실에서 느끼는 고통을 약 2배 이상 크게 느껴, 손실을 회피하려는 경향이 강하다.
-
인간은 확률을 객관적으로 평가하지 않고, 희박한 확률은 과대평가하며 거의 확실한 확률은 과소평가하는 경향을 보인다.
-
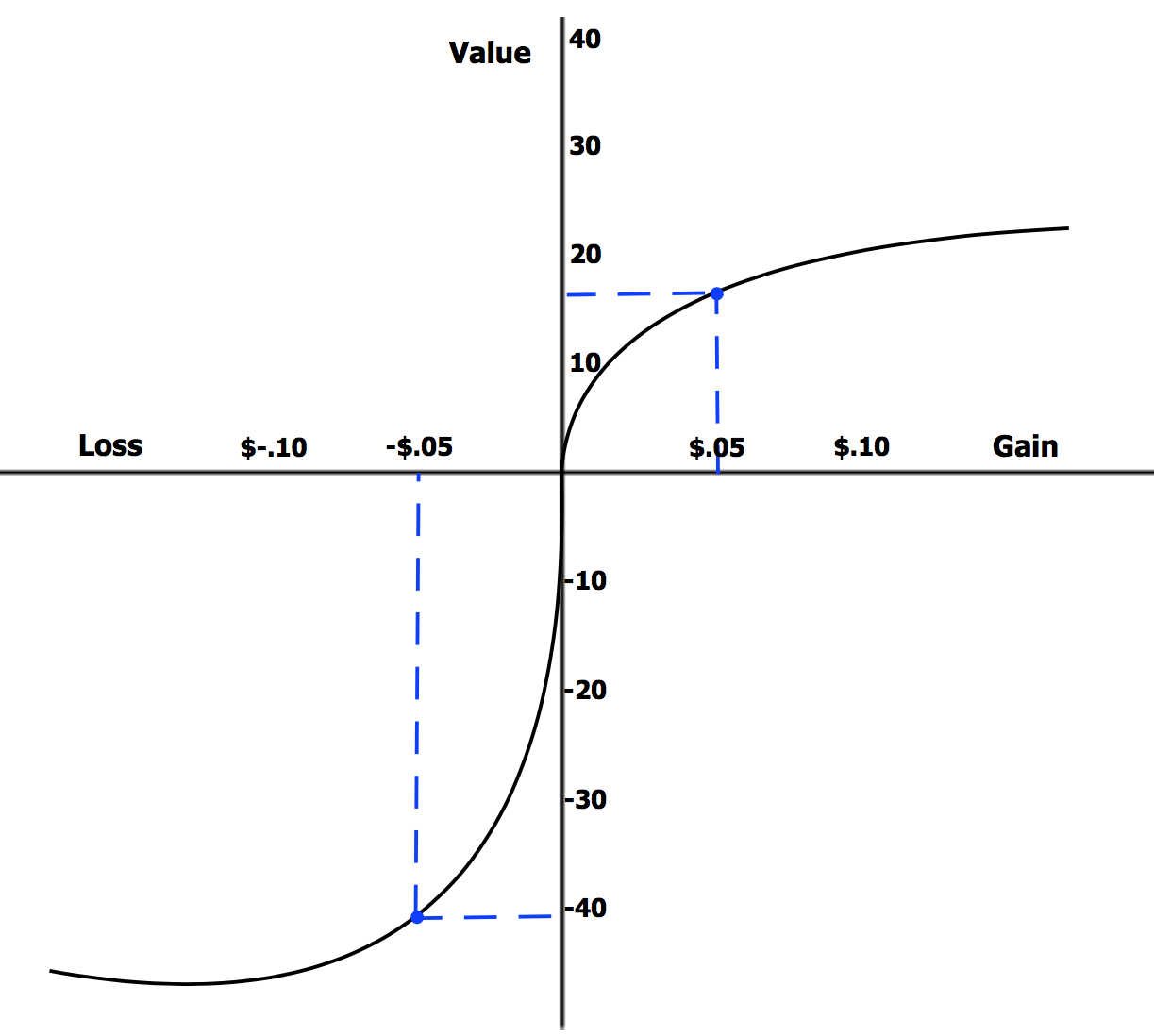
손실 영역(그래프 왼쪽)이 이익 영역(그래프 오른쪽)보다 훨씬 더 가파르다
가치 함수 (Value Function): 이익과 손실의 비대칭성
1) 기준점 의존성 (Reference Point Dependence)
- 사람들은 절대적인 부의 총량으로 행복을 느끼는 것이 아니라, 특정 기준점(reference point)으로부터의 변화를 통해 이익과 손실을 인식한다.
- 이 기준점은 현재 나의 자산 상태, 혹은 기대치 등이 될 수 있다.
- 비유: 연봉이 5천만 원인 사람이 1억 원을 벌게 되면 ‘5천만 원의 이익’으로 느끼지만,
- 원래 연봉이 2억 원이던 사람이 1억 원을 벌게 되면 ‘1억 원의 손실’로 느낀다.
- 결과는 ‘1억 원’으로 동일하지만, 기준점이 다르기 때문에 느끼는 가치는 하늘과 땅 차이다.
- 이 기준점은 현재 나의 자산 상태, 혹은 기대치 등이 될 수 있다.
2) 손실 회피성 (Loss Aversion)
- 가치 함수의 가장 두드러진 특징은 손실 영역의 그래프 기울기가 이익 영역보다 훨씬 가파르다는 점이다.
- 이는 동일한 금액이라도 이익에서 얻는 기쁨보다 손실에서 느끼는 고통이 훨씬 크다는 것을 의미한다.
- 연구에 따르면 그 고통은 약 2~2.5배 더 큰 것으로 알려져 있다.
- 비유: 길에서 1만 원을 주웠을 때의 기쁨보다, 지갑에서 1만 원을 잃어버렸을 때의 상실감이 두 배 이상 더 크게 다가온다.
- 그래서 사람들은 ‘이익을 얻으려는 노력’보다 ‘손실을 피하려는 노력’을 더 강하게 한다.
3) 민감도 체감성 (Diminishing Sensitivity)
- 그래프를 보면 이익이든 손실이든, 기준점에서 멀어질수록 곡선의 기울기가 완만해지는 것을 볼 수 있다.
- 이는 변화의 크기가 커질수록 그에 대한 민감도는 점차 둔해진다는 의미다.
- 비유: 10만 원을 벌었을 때의 기쁨은 0원에서 10만 원이 되었을 때 가장 크다.
- 하지만 이미 1,000만 원을 번 상태에서 추가로 10만 원을 더 버는 것은 처음만큼 기쁘지 않다.
- 손실의 경우도 마찬가지로, 1,000만 원을 잃은 사람이 추가로 10만 원을 더 잃는 것은 처음 10만 원을 잃었을 때만큼 고통스럽지 않다.
- 이는 변화의 크기가 커질수록 그에 대한 민감도는 점차 둔해진다는 의미다.
확률 가중 함수 (Probability Weighting Function): 확률의 주관적 왜곡
- 두 가지 특성 때문에 확률 가중 함수는 S자를 옆으로 눕힌 듯한 역 S자 형태를 띈다.
1) 낮은 확률의 과대평가
- 사람들은 실제로는 거의 일어나지 않을 희박한 확률(예: 0.1%, 1%)을 실제보다 훨씬 더 높게 평가하는 경향이 있다.
- 이러한 심리가 바로 ‘로또’ 구매로 이어진다.
- 당첨 확률이 극히 낮다는 것을 알면서도 ‘혹시 내가?‘라는 기대로 실제 확률보다 더 높은 가치를 부여하는 것이다.
2) 높은 확률의 과소평가
- 반대로, 거의 확실에 가까운 높은 확률(예: 99%)은 실제보다 낮게 평가하는 경향이 있다.
- ‘99% 안전’이라는 말보다 ‘1% 위험’이라는 말에 더 신경 쓰는 심리가 여기에 해당한다.
- 99% 확률의 이익은 ‘거의 확실한’ 것이 아니라 ‘혹시나 안 될 수도 있는 1%의 불확실성’ 때문에 그 가치가 깎여나간다.